ESTADÍSTICA I

PRIMERA SEMANA

NOCIONES DE ESTADÍSTICA DESCRIPTIVA

¿Qué es la estadística descriptiva?

El término estadística descriptiva se refiere al análisis, el resumen y la presentación de los resultados relacionados con un conjunto de datos derivados de una muestra o de toda la población. 

La estadística descriptiva comprende tres categorías principales: distribución de frecuencias, medidas de tendencia central y medidas de variabilidad.

Objetivo de la estadística descriptiva

El objetivo de la estadística descriptiva es describir los datos observados de forma sintética y significativa para poder analizarlos mejor. Es recoger observaciones sobre sujetos con una determinada propiedad y traducir estas observaciones en números que proporcionen información sobre dicha propiedad.

En resumen, su objetivo es estructurar y representar la información contenida en los datos.

Importancia de la estadística descriptiva

La estadística descriptiva facilita la visualización de los datos. Permiten presentarlos de forma significativa y comprensible, lo que a su vez da pie a una interpretación simplificada del conjunto de datos en cuestión. 

Los datos brutos serían difíciles de analizar, y la determinación de tendencias y patrones puede ser un reto. Además, los datos en bruto dificultan la visualización de lo que muestran los datos.

Tipos de estadística descriptiva

La estadística descriptiva ayuda a describir y comprender las características de un conjunto de datos específico ofreciendo breves resúmenes sobre la muestra y las medidas de los datos. 

Estos son los tipos de estadística descriptiva:

– Distribución de frecuencias

Utilizada tanto para datos cualitativos y cuantitativos. Representa la frecuencia o el recuento de los diferentes resultados en un conjunto de datos o muestras. 

La distribución de frecuencias se presenta normalmente en una tabla o un gráfico. Cada entrada de la tabla o el gráfico va acompañada del recuento o la frecuencia de aparición de los valores, en un intervalo, rango o grupo específico.

La distribución de frecuencias es básicamente una presentación o un resumen de datos agrupados que se han clasificado en función de clases mutuamente excluyentes y del número de ocurrencias en cada clase respectiva. Permite una forma más estructurada y organizada de presentar los datos en bruto.

Los cuadros y gráficos más comunes utilizados en la presentación y visualización de la distribución de frecuencias incluyen gráficos de barras, histogramas, gráficos circulares y gráficos de líneas.

¿Qué es una tabla de frecuencias?

Una tabla de frecuencias muestra de forma ordenada un conjunto de datos estadísticos y a cada uno de ellos le asigna una frecuencia que, en pocas palabras, son las veces que se repite un número o dato. 

Puedes usar las tablas de frecuencias para ordenar variables cuantitativas o cualitativas.

Tipos de frecuencias

• Frecuencias absolutas: son el número de veces que se repite un número en un conjunto de datos.
• Frecuencias absolutas acumuladas: es la suma de las frecuencias absolutas.
• Frecuencia relativa: corresponde a las veces que se repite un número en un conjunto de datos respecto al total, pero se expresa en porcentajes (%).
• Frecuencia relativa acumulada: es la suma de las frecuencias relativas.

¿Cómo construir una tabla de frecuencias?

¡Vamos a tomar como ejemplo un salón de clases! Imagina que eres profesor o profesora de biología de 20 estudiantes y tienes las notas finales del semestre.

Sigue estos pasos para construir tu tabla de frecuencias:

Paso 1:

Reúne los datos.

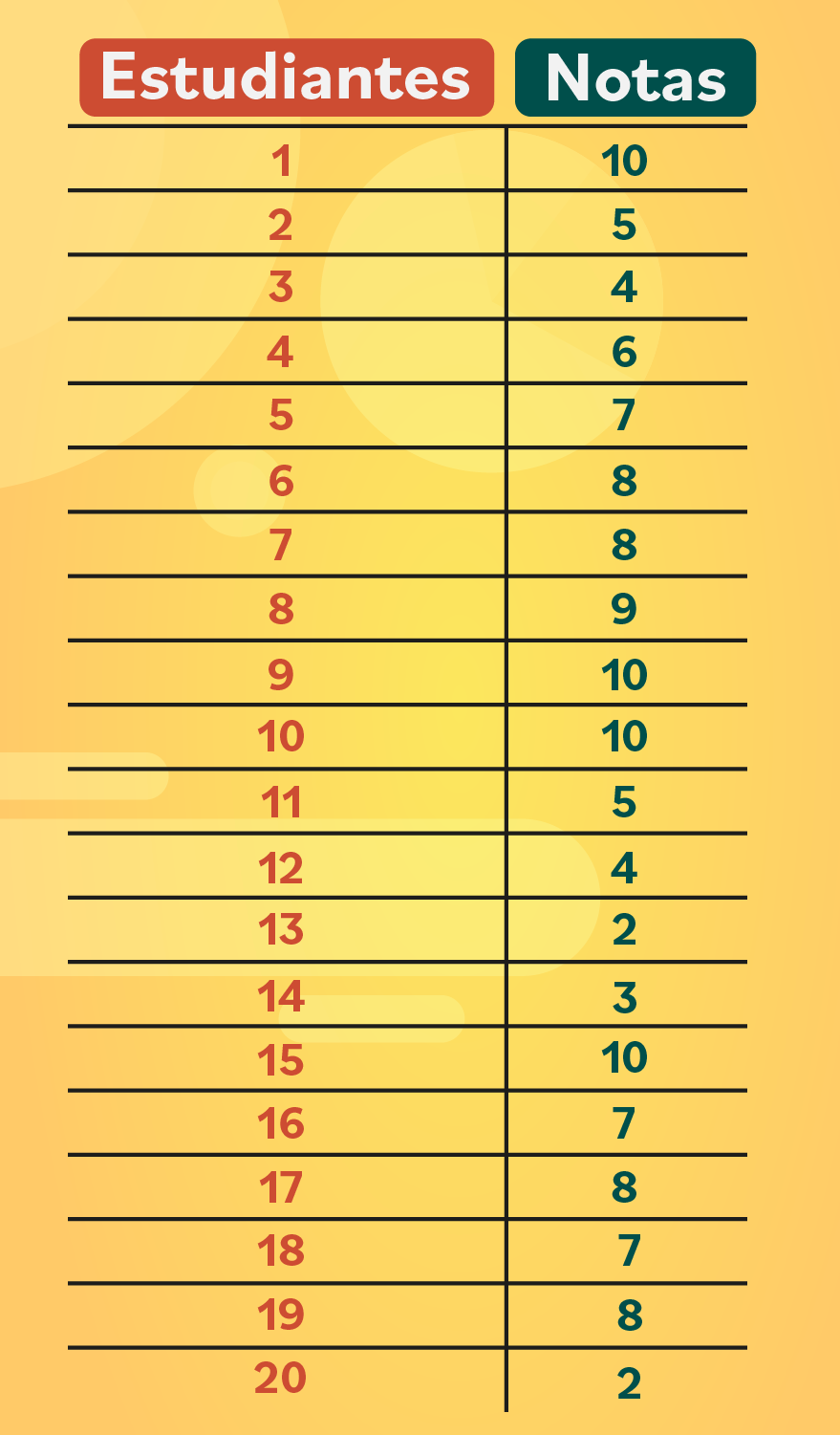
Paso 2:

Crea una nueva tabla. En la primera columna, ubica las notas de 1 a 10, de menor a mayor. En la segunda columna, escribe la cantidad de veces que se repite cada nota y llama a estos datos frecuencia absoluta.

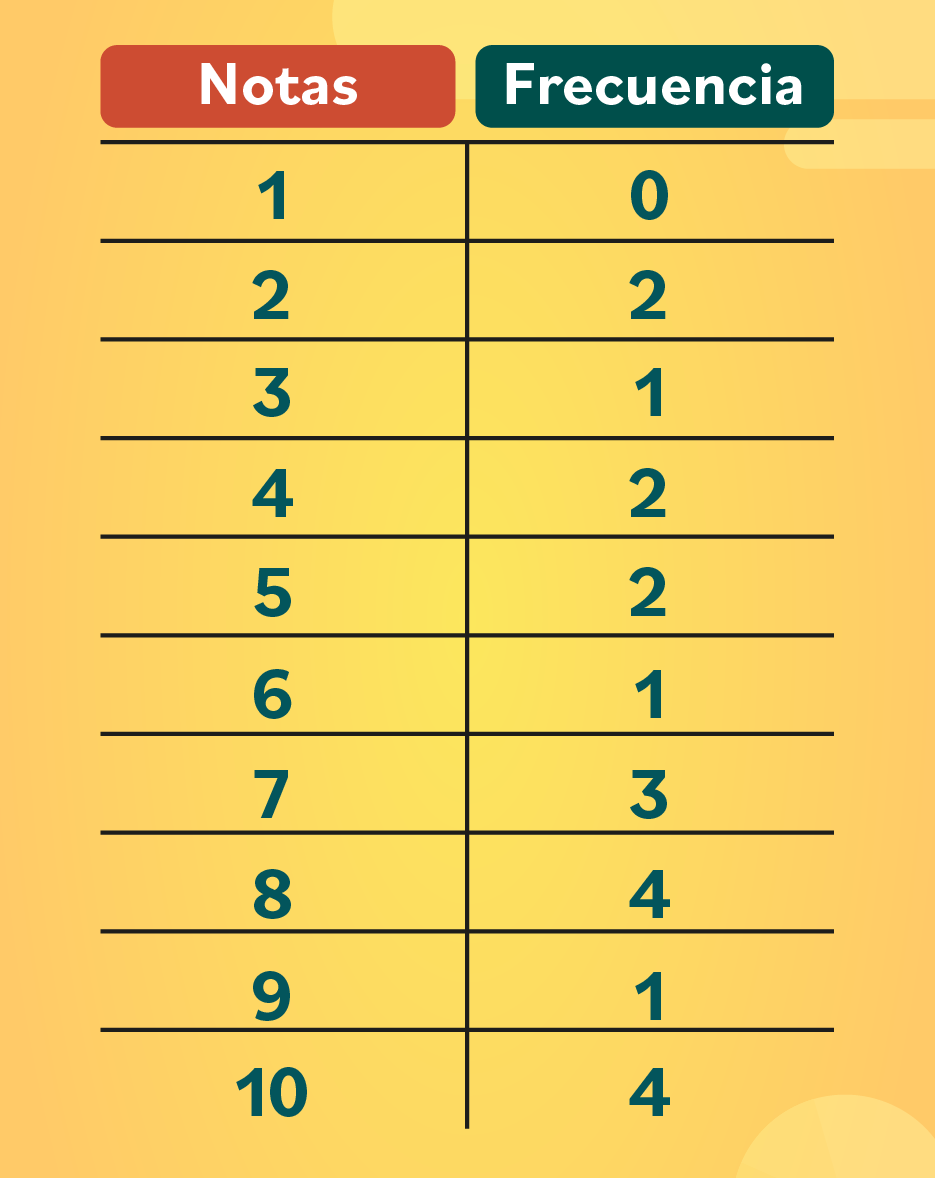
Paso 3:

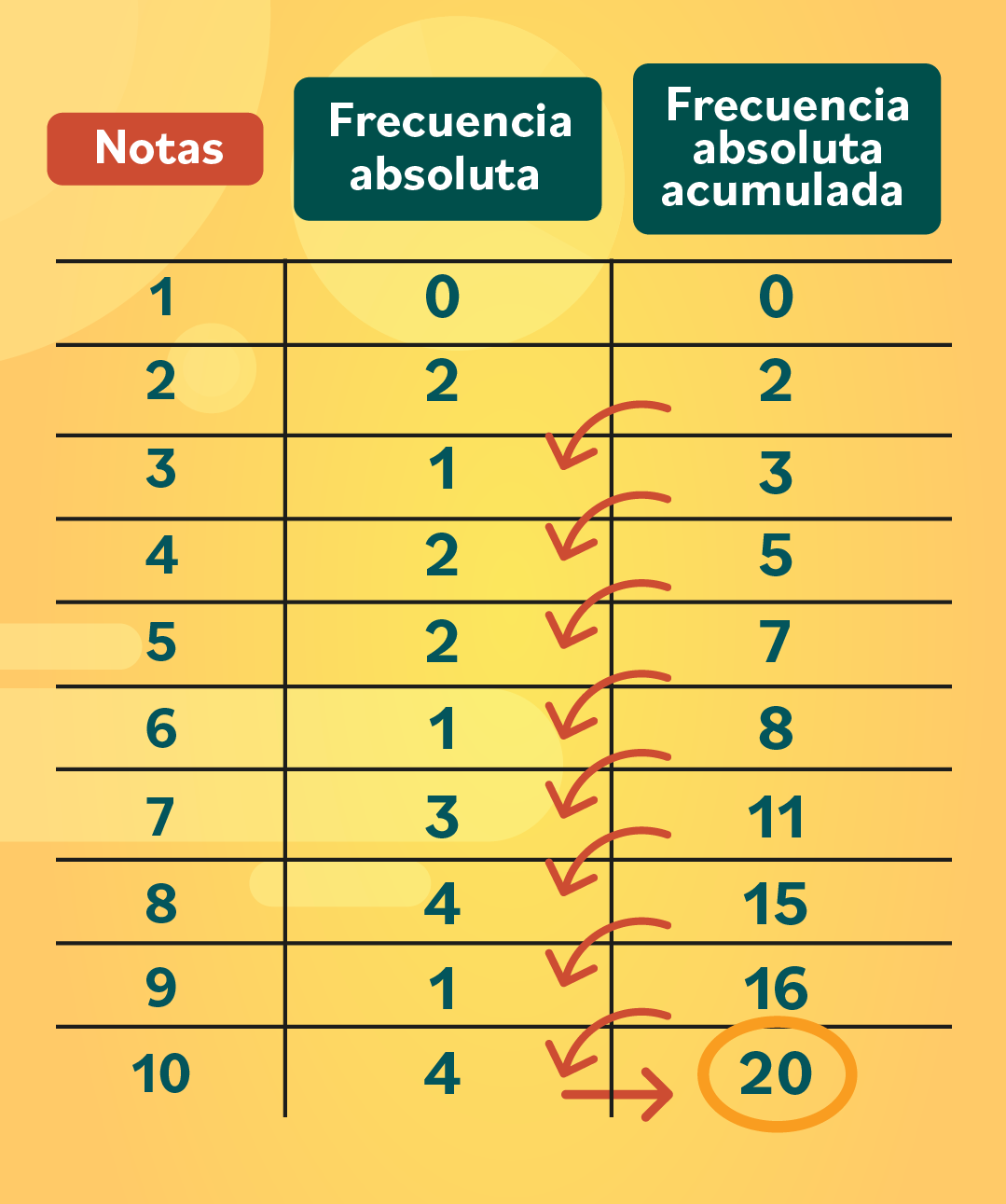
Hasta aquí tienes una tabla de frecuencias sencilla, pero también puedes agregarle una columna más para calcular la frecuencia absoluta acumulada. Sus valores se obtienen sumando los datos en diagonal. 

Por ejemplo: el primer número siempre va a  ser igual al primer dato de la frecuencia absoluta, en este caso es cero. Luego, para obtener el segundo dato, necesitas sumar el cero con el dos, que es el segundo número de la frecuencia absoluta y justamente, el que está ubicado de forma diagonal. Entonces: 0 + 2 = 2.

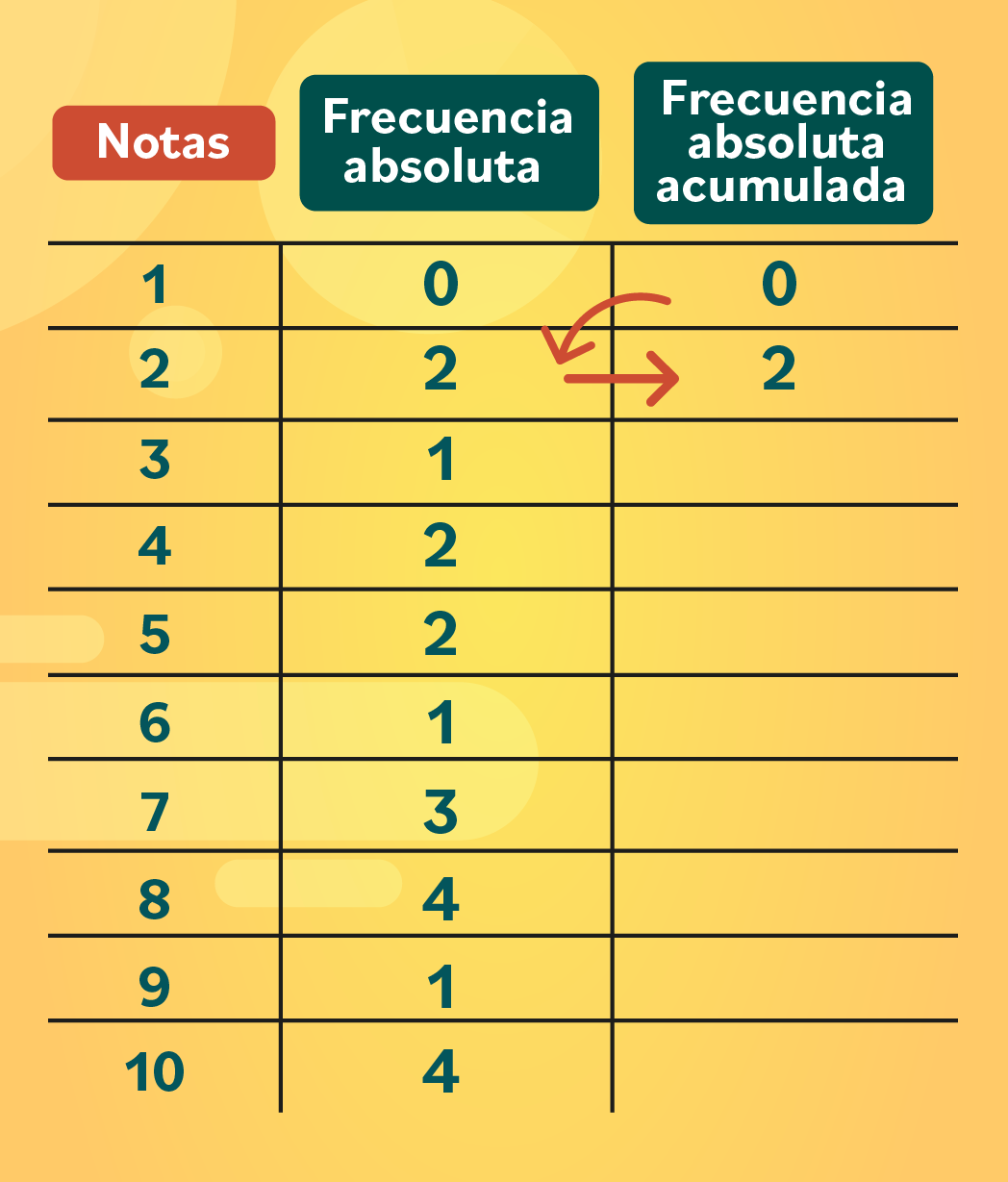
Paso 4:

Sigue sumando los números en diagonal. Ahora es el turno de 2 + 1 = 3. Continua hasta llenar toda la columna.

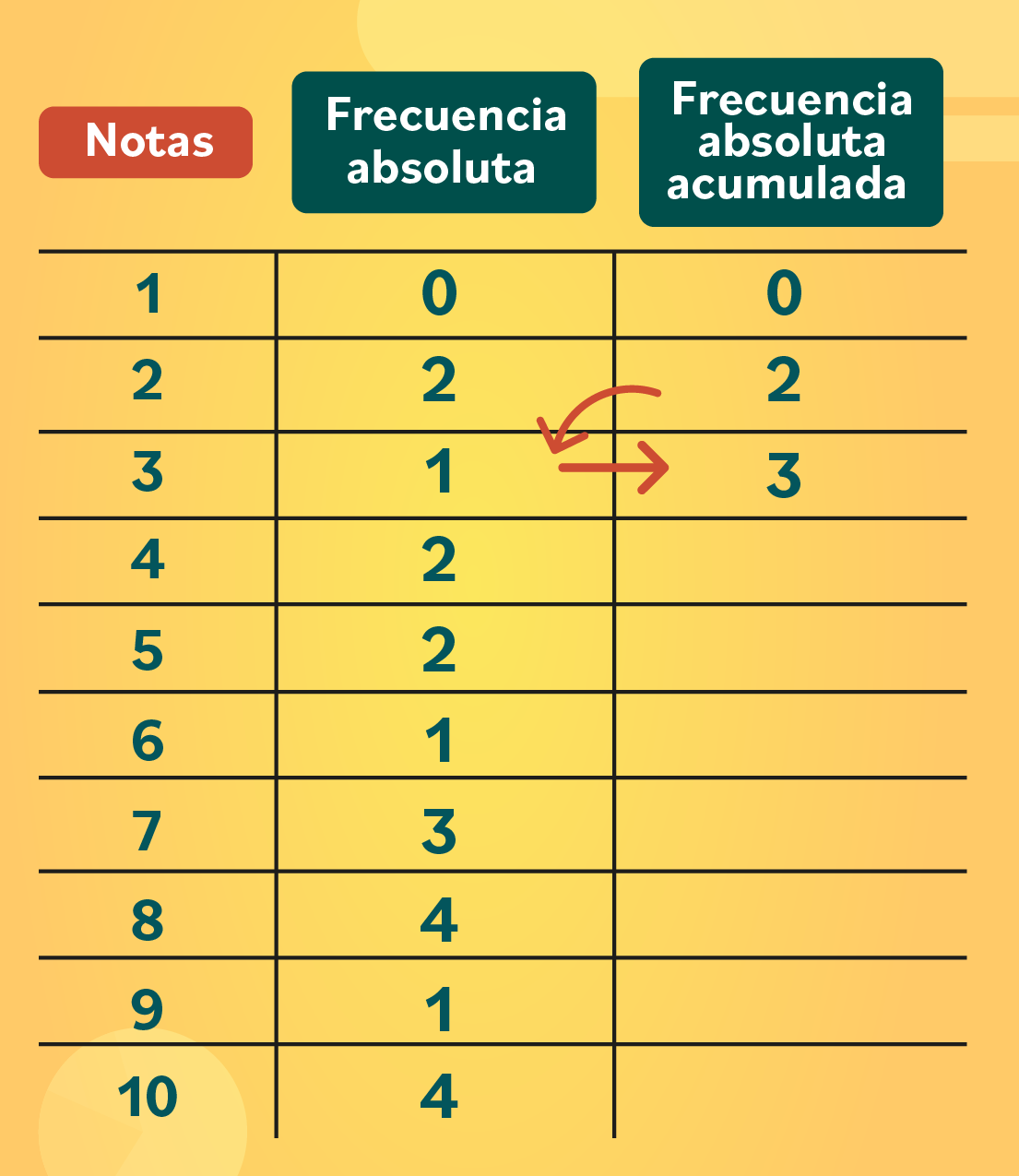
Paso 5:

Una forma de verificar que la suma es correcta, es obteniendo como número final la cantidad de datos que tienes. En este caso, sería igual a 20, porque son las notas de 20 estudiantes. ¡Y listo!

Frecuencia relativa y la frecuencia relativa absoluta

Al inicio de esta página, te explicamos que la frecuencia relativa se expresa en porcentajes. Mira cómo puedes obtenerlos a partir de los datos que ya tienes.

Paso 1: 

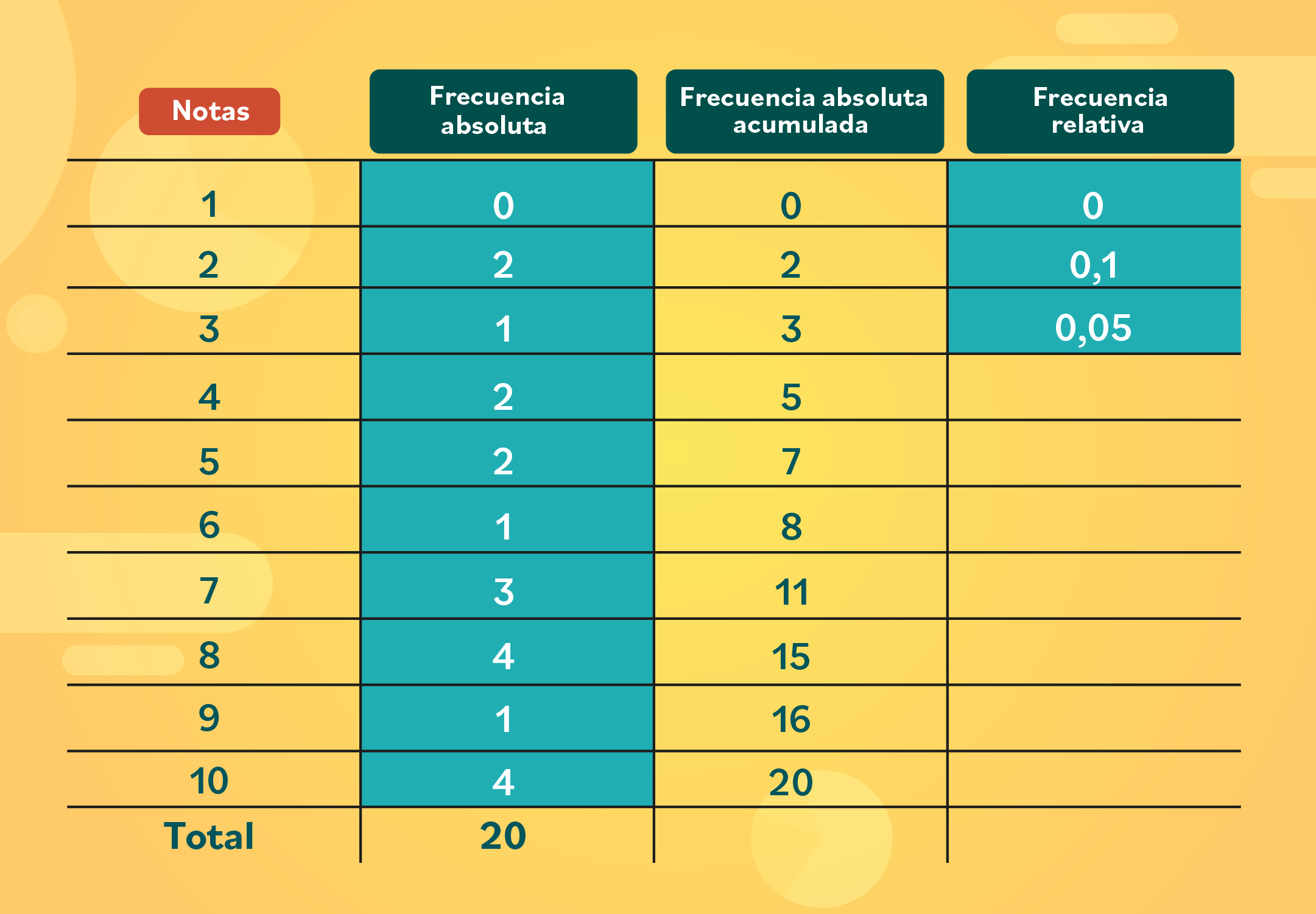
¡Continuemos con la tabla de frecuencias del salón de clases! Añade una cuarta columna con el nombre frecuencia relativa. Toma cada dato de la frecuencia absoluta y divídelo en 20, que es la cantidad de datos totales que tienes. Así:

                         0 ÷ 20 = 0                      2 ÷ 20 = 0,1                    1 ÷ 20 = 0,05

Paso 2:

Realiza las divisiones hasta obtener todos los datos. Al final, la suma de esos valores debe darte 1.

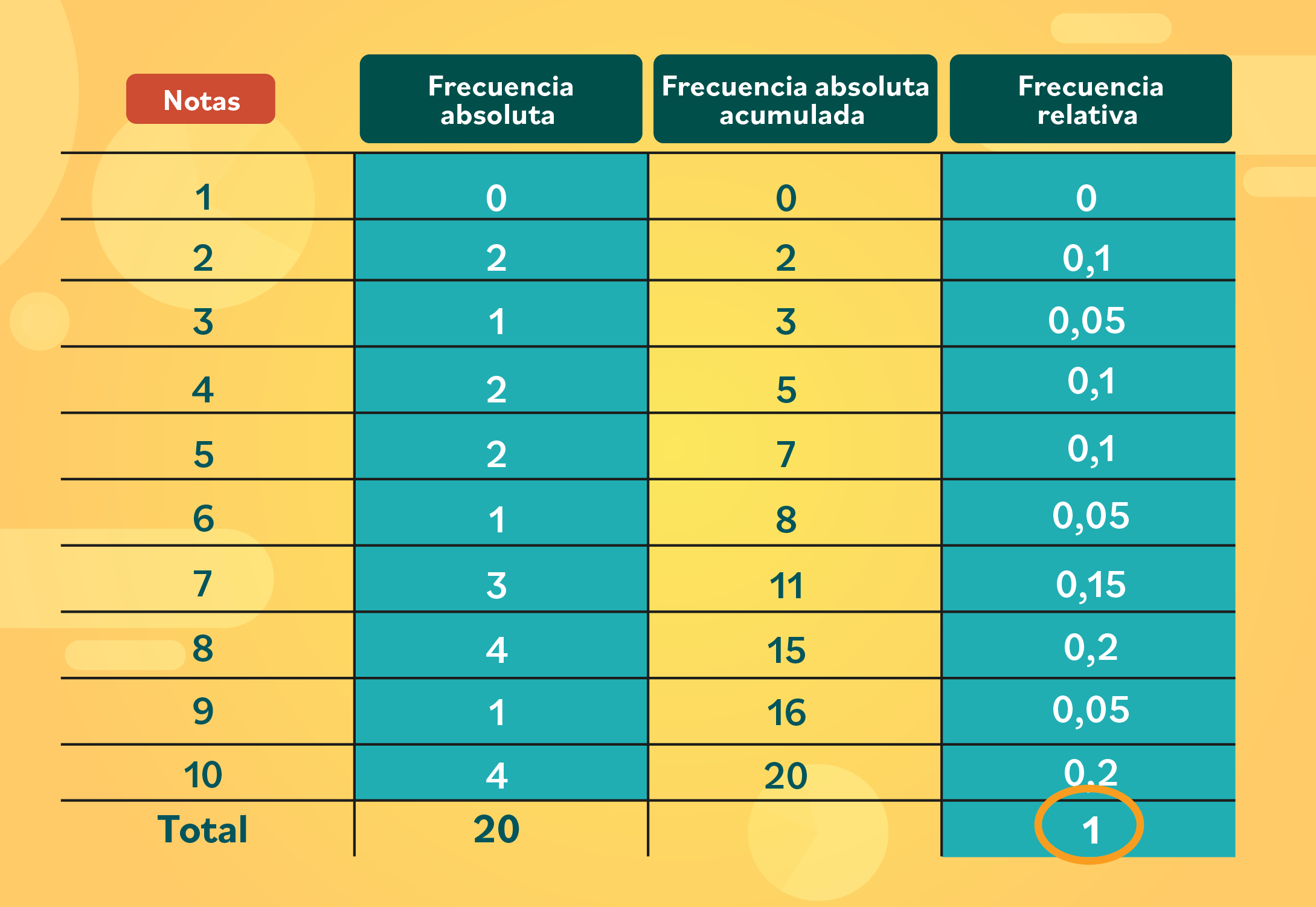
Si al sumar el resultado que obtienes es 0,98 o un número similar, no te preocupes, puedes aproximarlo a 1. 

Paso 3: 

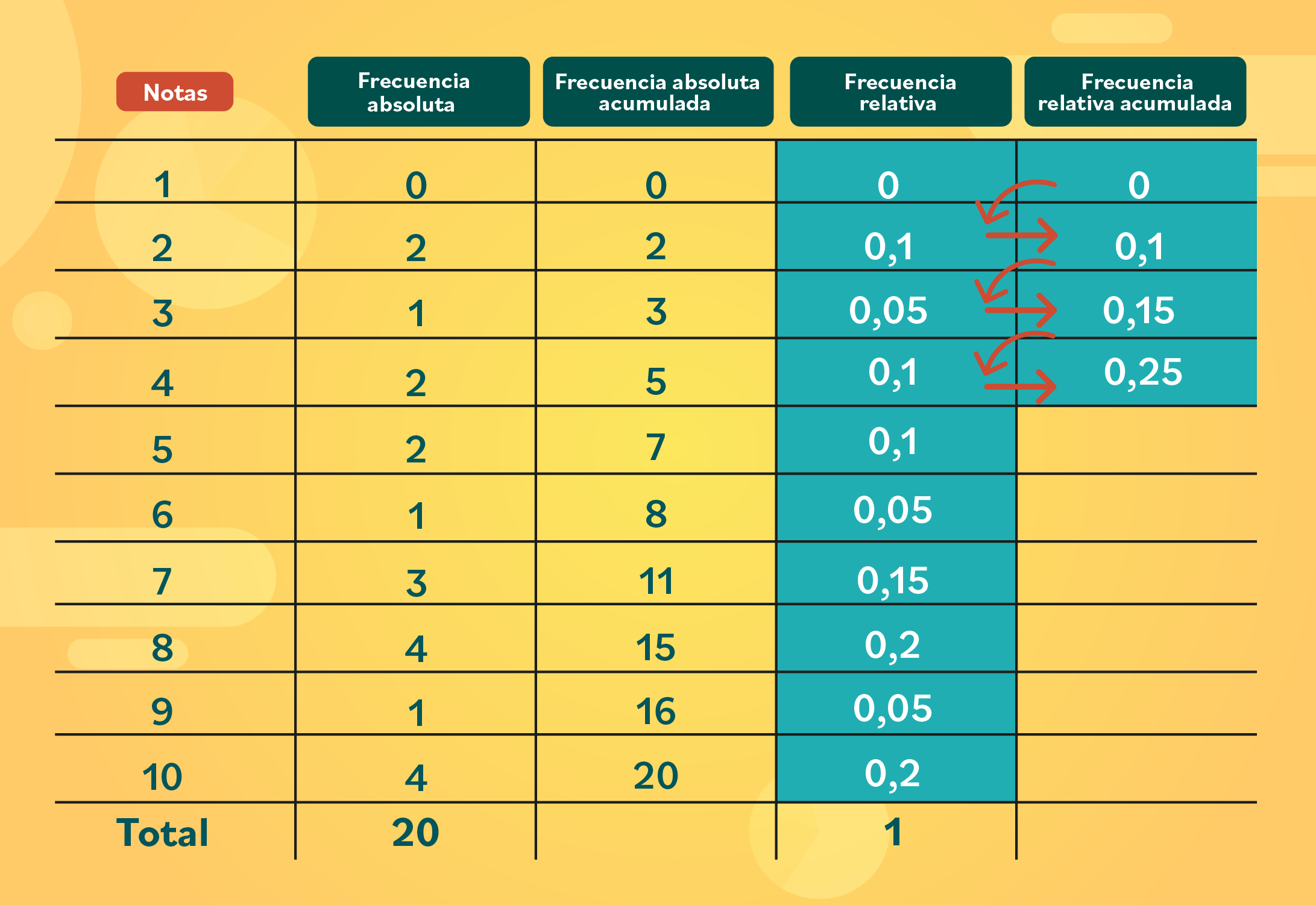
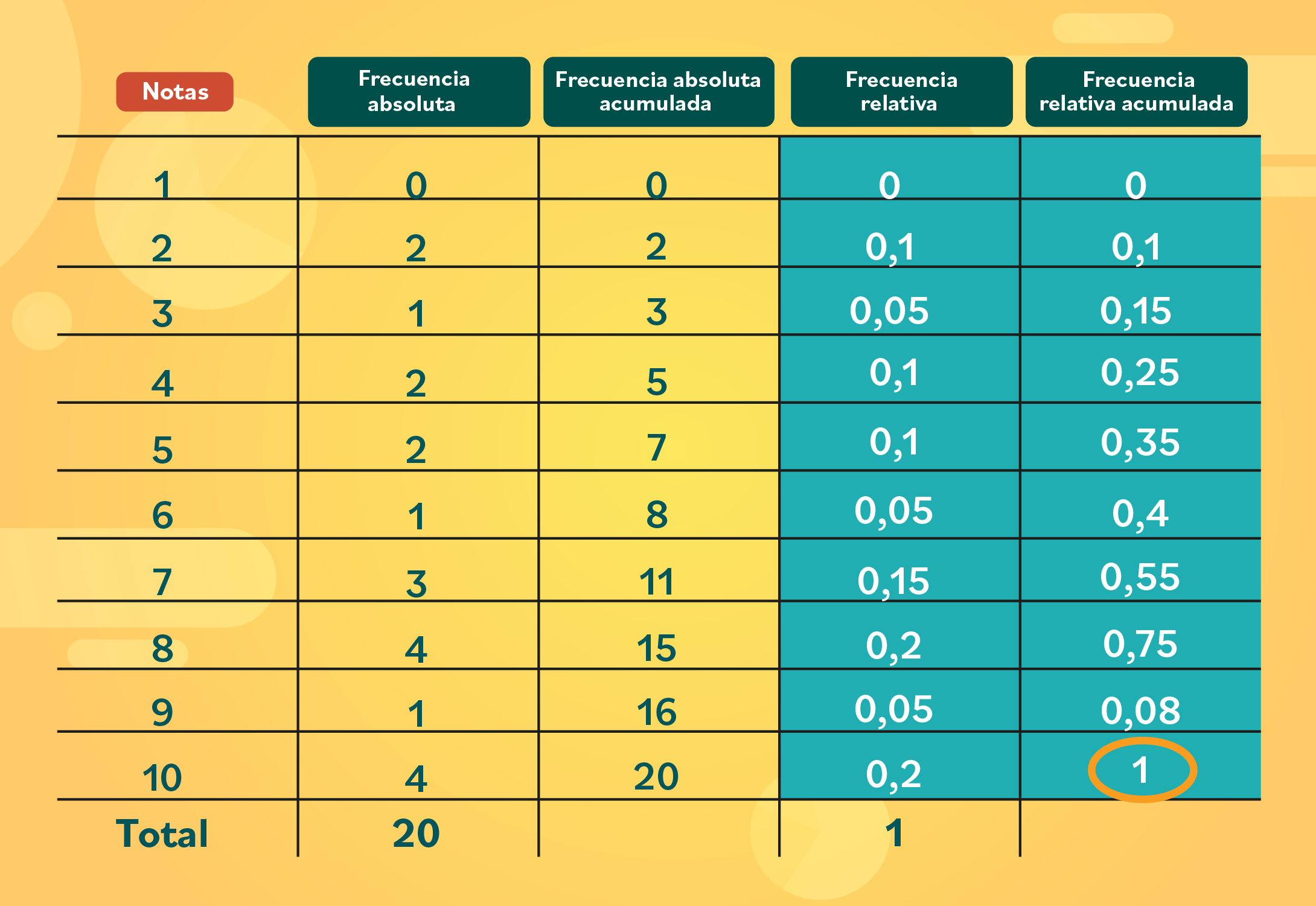
Para la frecuencia relativa acumulada debes sumar los datos en diagonal, como lo hicimos para la frecuencia absoluta acumulada.

Entonces, el primer número siempre va a  ser igual al primer dato de la frecuencia relativa, en este caso es cero. Luego, para obtener el segundo dato, necesitas sumar el cero con el 0,1, que es el segundo número de la frecuencia relativa y justamente, el que está ubicado de forma diagonal. Así:

                         0 + 0,1 = 0,1                      0,1 + 0,05 = 0,15                    0,15 +  0,1 = 0,25

Paso 4:

Suma todos los datos en diagonal hasta llenar toda la columna. El último número que obtengas debe ser 1.

Paso 5: 

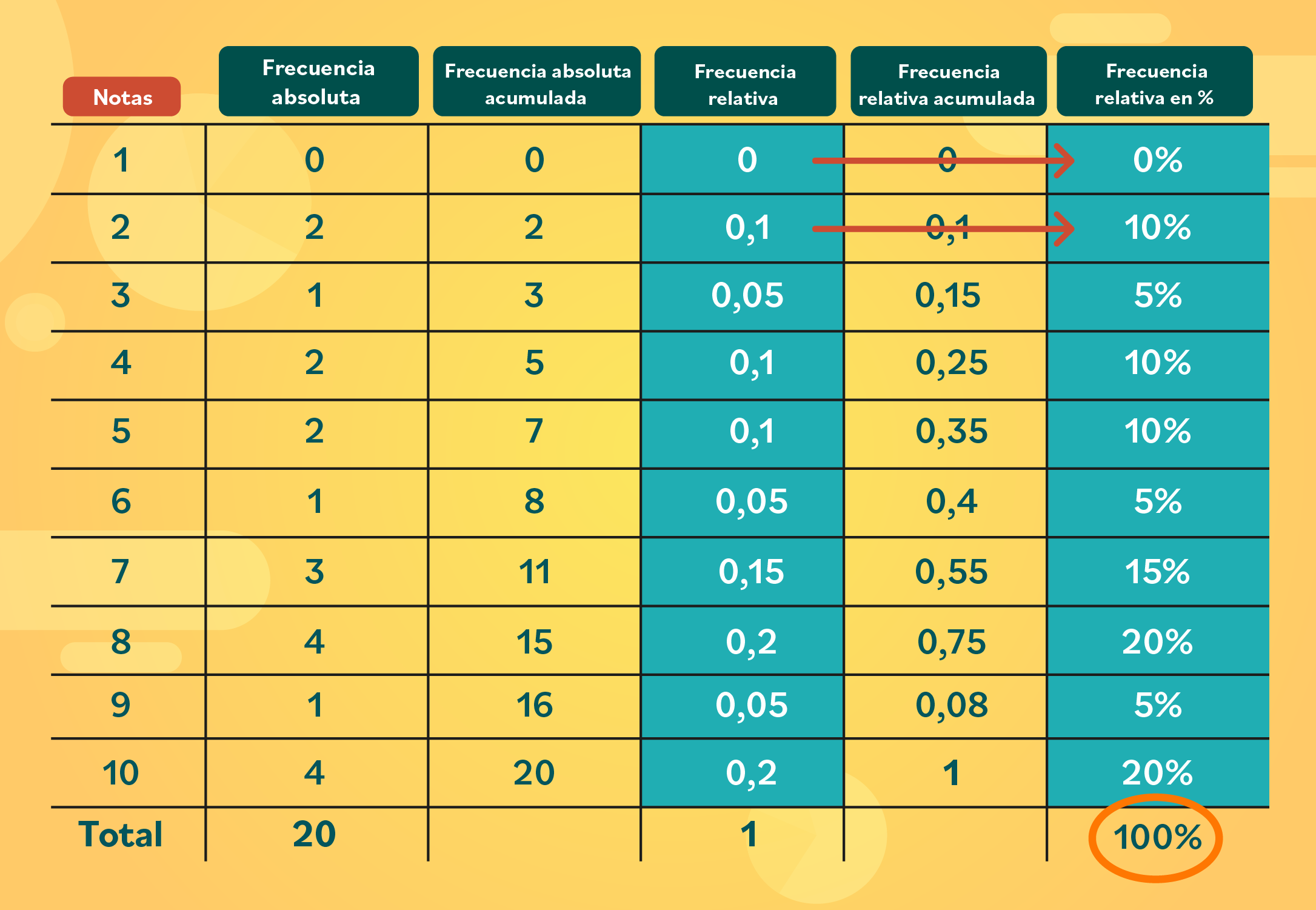
¡Ahora sí vamos a descubrir los porcentajes de la frecuencia relativa! Toma cada valor de la columna frecuencia relativa y multiplícalo por 100. Por ejemplo:

                              0 x 100 = 0                   0,1 x 100 = 10                0,05 x 100 = 5

Al final, la suma de esa columna debe dar 100 %.

Paso 6: 

Para terminar, calcula el porcentaje de la frecuencia relativa acumulada en porcentajes. Sus valores se obtienen sumando los datos en diagonal. 

Por ejemplo: el primer número siempre va a  ser igual al primer dato de la frecuencia relativa en %, es decir, a cero por ciento. Luego, para obtener el segundo dato, necesitas sumar el cero con el 10%, que es el segundo número de la frecuencia relativa  y  el que está ubicado de forma diagonal. Entonces: 0 + 10 = 10. Continúa:

                    10 + 5 = 15%                    15 + 10 = 25%                    25 +  10 = 35%

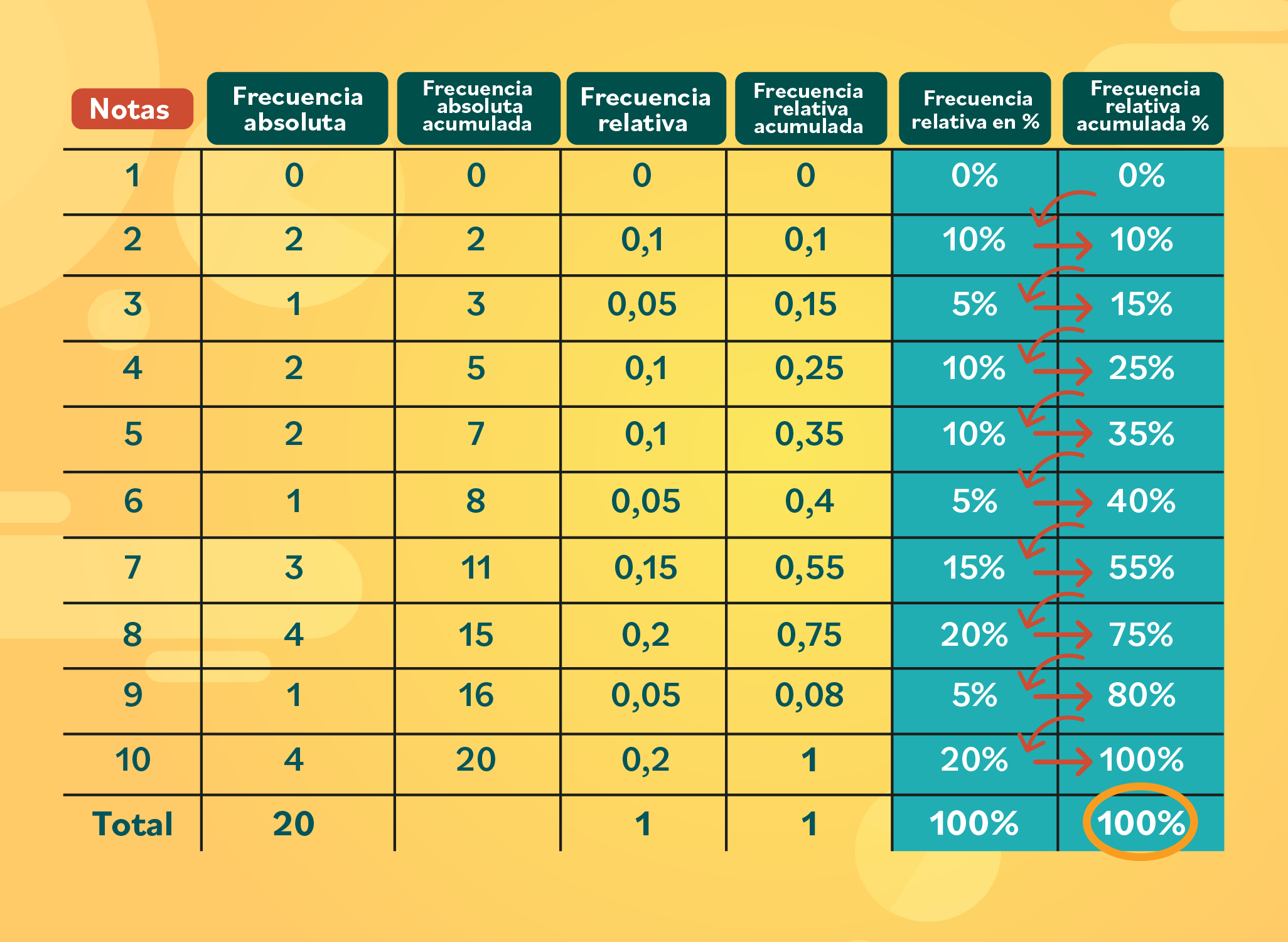
El último número que obtengas debe ser 100%.

Así de fácil puedes crear tu propia tabla de frecuencias. Solo recuerda:

• 1.- Reunir tus datos y organizarlos.
• 2.- Calcular la cantidad de veces que se repite un dato para obtener la frecuencia absoluta.
• 3.- Sumar los valores diagonalmente para obtener las   frecuencias acumuladas.
• 4.- La frecuencia relativa se expresa en porcentajes.

¿Qué es un gráfico de barras?

Un diagrama de barras es un gráfico usado para mostrar de forma resumida un grupo de datos que puede incluir variables cualitativas y cuantitativas.  

En este video te enseñamos como construir este tipo de diagramas:

Características de un diagrama de barras

• Se compone de columnas o barras de diferentes alturas, estas pueden ser horizontales o verticales.
• Tiene un eje horizontal o eje x, donde se ubica una variable, por lo general, cualitativa.
• Tiene un eje vertical o eje y, donde se ponen los valores que determinan la altura de las barras. A estos números se les conoce como frecuencia. 
• El ancho de las barras y el espacio entre cada una debe ser el mismo.
• Las barras también sirven para comparar valores.

¿Cómo se construye un gráfico de barras?

Para la fiesta de cumpleaños de Daniel su mamá decidió comprar varios sabores de helado. Solo tiene dinero para tres, así que le preguntará a cada invitado cuál es su sabor favorito entre:

•  Chocolate
• Vainilla
• Fresa
• Brownie 
• Chicle

Paso 1:

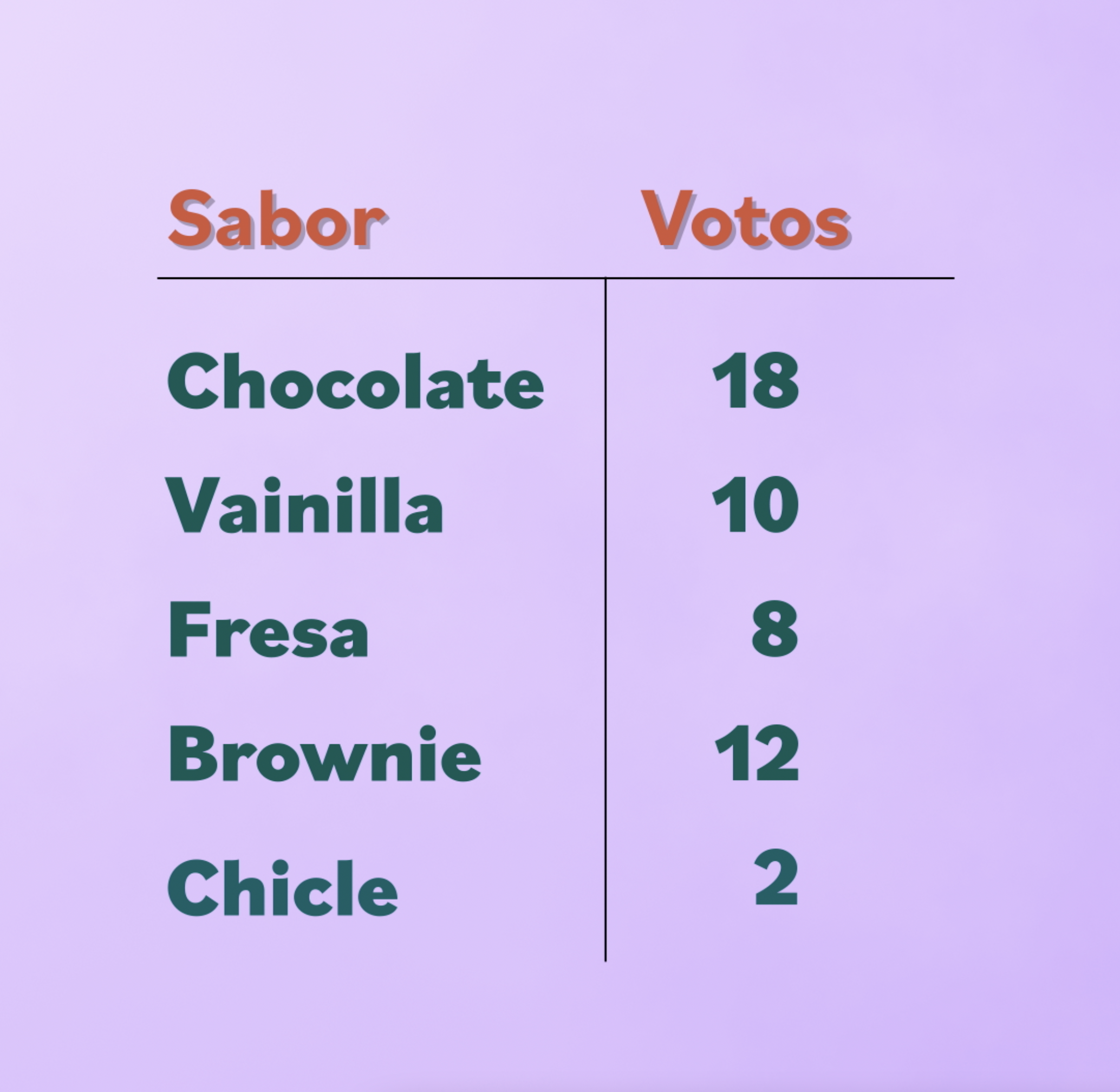
Con las respuestas de los 50 invitados, organiza los siguientes datos en una tabla: 18 personas votaron por el helado de chocolate, 10 por vainilla, 12 por brownie, 8 por fresa y 2 por chicle.

Recuerda que a las veces que se repite un dato se le llama Frecuencia.

Paso 2:

Ubica en el eje x cada uno de los sabores.

Paso 3:

En el eje y coloca la cantidad de personas que votaron por cada sabor. Como el número mayor es el 18, puedes usar una frecuencia de números de dos en dos. Así: dos, cuatro, seis, ocho, diez, doce, catorce, dieciséis y diez y ocho. 

La clave para elegir los números del eje y está en identificar el número más grande. Si tuvieras cifras de 200 o 355 invitados, colocar los números de dos en dos haría que la gráfica quede muy alta. En estos casos, busca una frecuencia que se acomode a lo que quieres mostrar, puede que usar números de de 50 en 50, te funcione mucho mejor.

Paso 4:

Ubica las barra en dirección a donde hayas ubicado cada sabor. Su tamaño depende del número de personas que votaron. Por ejemplo, la barra de chocolate llega hasta el número 18; la de vainilla, hasta diez; y así sucesivamente hasta utilizar todos los datos de la tabla. 

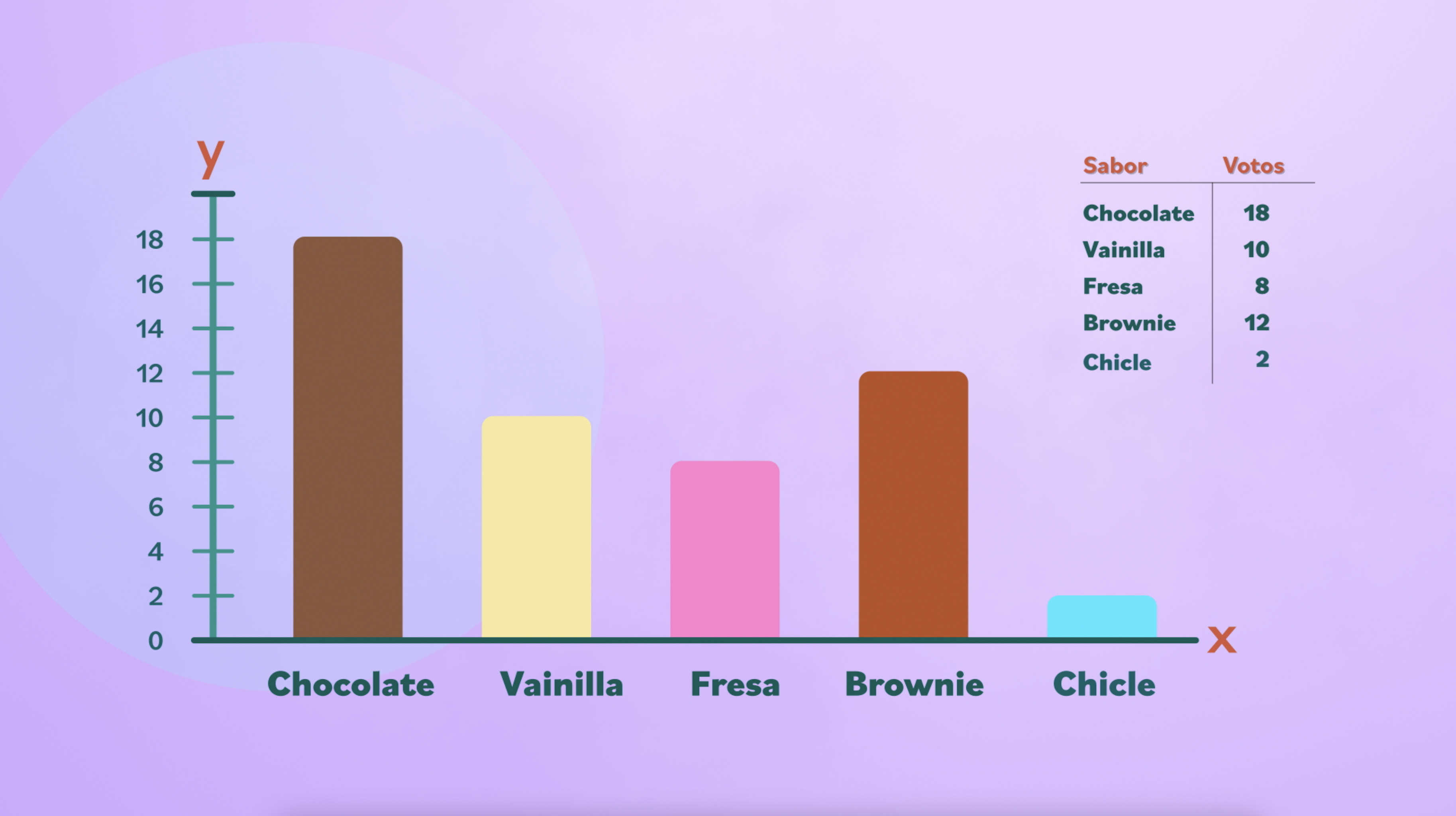
Paso 5:

¡Eso es todo! Con este diagrama la mamá de Daniel puede explicarle a su hijo porque los sabores de helado comprarán son: vainilla, chocolate y brownie. Después de todo, ¡son los que le gustan a la mayoría!

Si quieres aprender a construir otro tipo de gráficos como el diagrama circular o lineal, ¡no te pierdas las siguientes páginas! 

Gráfico de torta o diagrama circular

Los diagramas circulares también son llamados gráficos de torta, tarta, pizza o 360 grados, porque se dividen en porciones. 

Características de un diagrama circular:

• Estos gráficos sólo representan y comparan una variable. 
• A cada cualidad de la variable le pertenece una porción del gráfico. 
• Las cifras que se anotan sobre cada trozo se expresan en porcentajes, por eso son útiles cuando la información que tienes es en su mayoría numérica y son pocos datos.
• La unión de todos los sectores forman un círculo completo. 
• Se usa para expresar proporcionalmente los distintos valores de la frecuencia de las variables.

¿Cómo se construye un diagrama circular?

En el equipo de baloncesto de Juliana mandarán a confeccionar unas chaquetas para el campeonato regional. La entrenadora quiere usar un diagrama circular para mostrarle a la junta la cantidad de deportistas por talla y así, lograr que le aprueben el presupuesto.

Paso 1:

Empieza por organizar los datos en una tabla. En la primera columna escribe las tallas: XS, S, M y L. 

Paso 2:

Crea una segunda columna llamada frecuencia. Aquí debes escribir la cantidad de jugadoras que usan cada talla: 5 atletas usan XS, 10 prefieren la talla S, 26 la M y 19 la L. Al sumar estos datos debes obtener el número total de jugadoras, son 60.

Recuerda que en la frecuencia se ubican las variables cuantitativas que estás usando. En este caso, la cantidad de jugadoras por talla.

Paso 3:

En una tercera columna, escribe los grados. Para calcularlos, toma los 360 grados que componen un círculo completo y divídelos entre las 60 jugadoras. 

                                                                                  360 ÷ 60 = 6

Así sabrás que a cada deportista le corresponden 6 grados del círculo.

Paso 4: 

Multiplica los 6 grados de cada jugadora  por la cantidad de deportistas que usan cada talla. 

6 x 5 = 30   ➟ Esto significa que la talla XS representa 30° del círculo.

6 x 10 = 60 ➟ A la talla S le corresponde un trozo de 60°.

6 x 26 = 156  ➟ La talla M representa 156°.

6 x 19 = 114  ➟ A la talla L le corresponde un trozo de 114°.

En la tabla los datos se verían así:

Paso 5:

Para comprobar que la división de grados es correcta, solo debes sumar los datos de la columna y obtener como resultado: 360 grados. Así confirmarás que ninguna parte del círculo quedó por fuera.

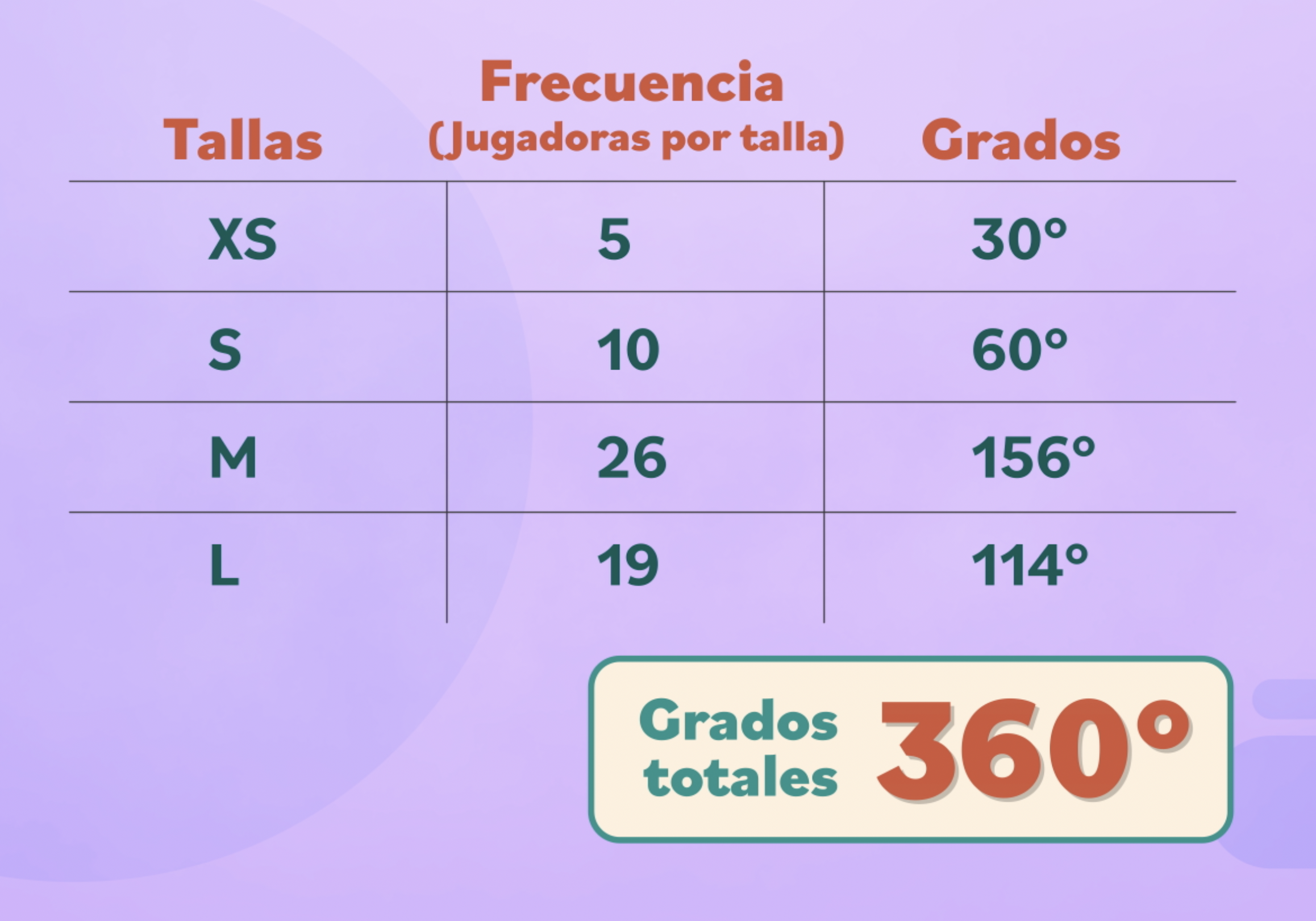
Paso 6:

Añade una cuarta columna para calcular los porcentajes de cada número de la frecuencia. Toma el 100% que representa el total y divídelo en 60 para saber qué porcentaje le corresponde a cada jugadora.

                                                                        100 ÷ 60 = 1,7

A cada deportista le corresponde el 1,7%.

Ten en cuenta que el 100% siempre representa el total.

Paso 7:

Multiplica el 1,7 por la cantidad de jugadoras que usan cada talla. 

1,7 x 5 = 8,5 ➟ Talla XS

1,7 x 10 = 17 ➟ Talla S

1,7 x 26 = 44,2 ➟ Talla M

1,7 x 19 = 32,3 ➟ Talla L

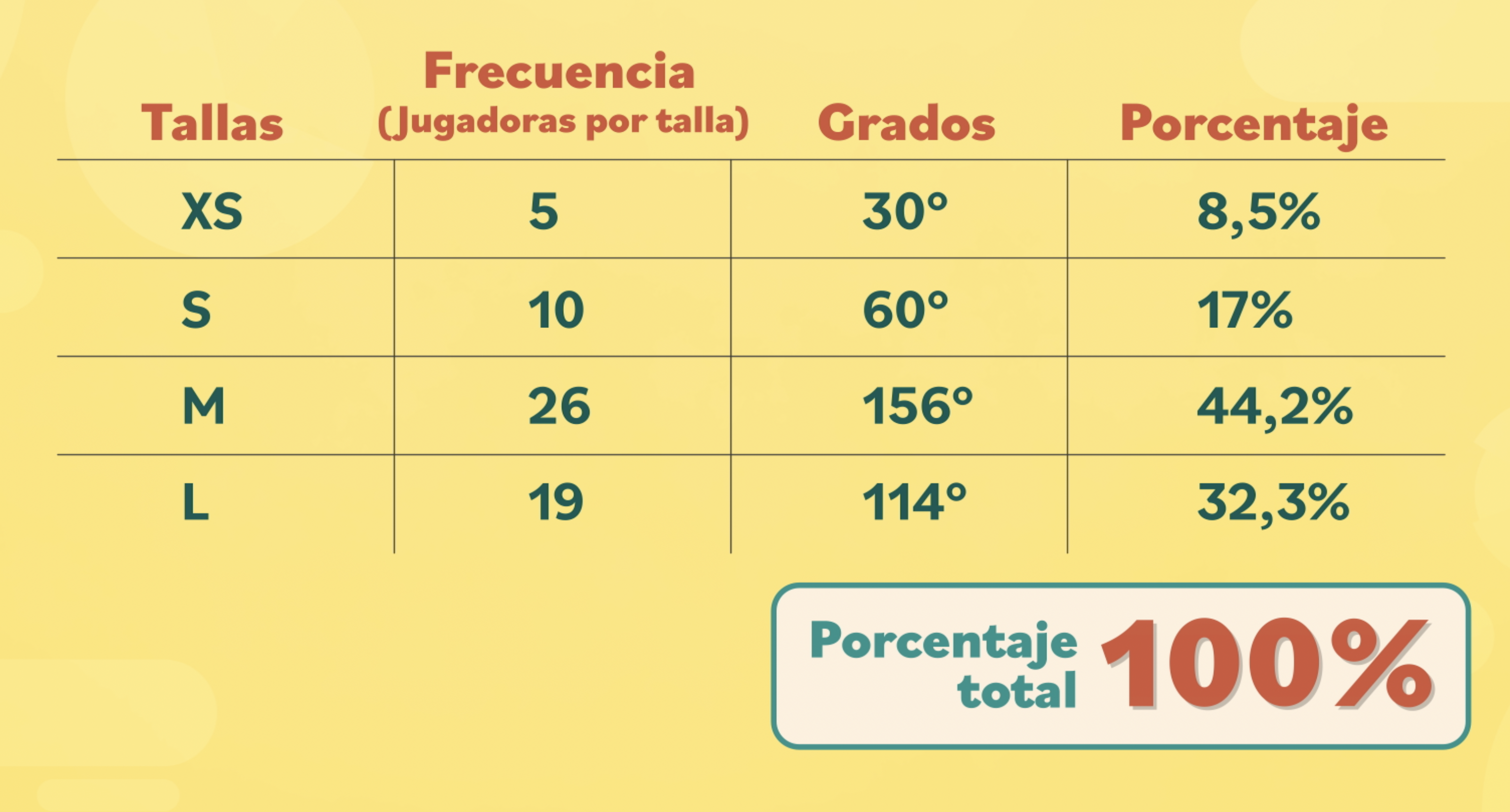
Paso 8:

Añade los datos a la tabla. La suma de esta columna debe dar 100%. No te preocupes si el resultado se pasa por uno o dos números, esto suele pasar porque en la división los decimales se aproximan.

Paso 9:

¡Es momento de graficar! Dibuja un círculo y con ayuda de un transportador traza los primeros 30 grados. Continúa con los 60 grados de la talla S. Luego, con los 156 de la talla M y, por último, la talla L con 144 grados.

Paso 10:

Ahora, añade a cada trozo el porcentaje correspondiente, ¡y listo! 

La entrenadora tiene una herramienta muy sencilla para explicarle a la junta porque necesitan más tela de la pensada, pues la mayoría de deportistas usan las tallas más grandes.

Gráfico lineal

El diagrama o gráfico lineal se compone de una serie de puntos que al unirlos te muestran una línea completa con los cambios de una variable a lo largo del tiempo.

En este gráfico, los datos no se representan con barras o por trozos, si no con puntos ubicados en el cruce de un eje x,  que representa la variable del tiempo, y un eje y, donde se ubica la variable continua que estás estudiando, como el tamaño de una mascota, por ejemplo.

Este tipo de diagramas son muy útiles cuando cuentas con una variable cuantitativa y quieres ver su comportamiento en el transcurso del tiempo.  

¿Cómo construir un diagrama lineal?

Vamos a crear un gráfico que muestre el avance de la construcción de una pequeña ciudad que promete ser la más innovadora del mundo.

Tenemos los siguientes datos:

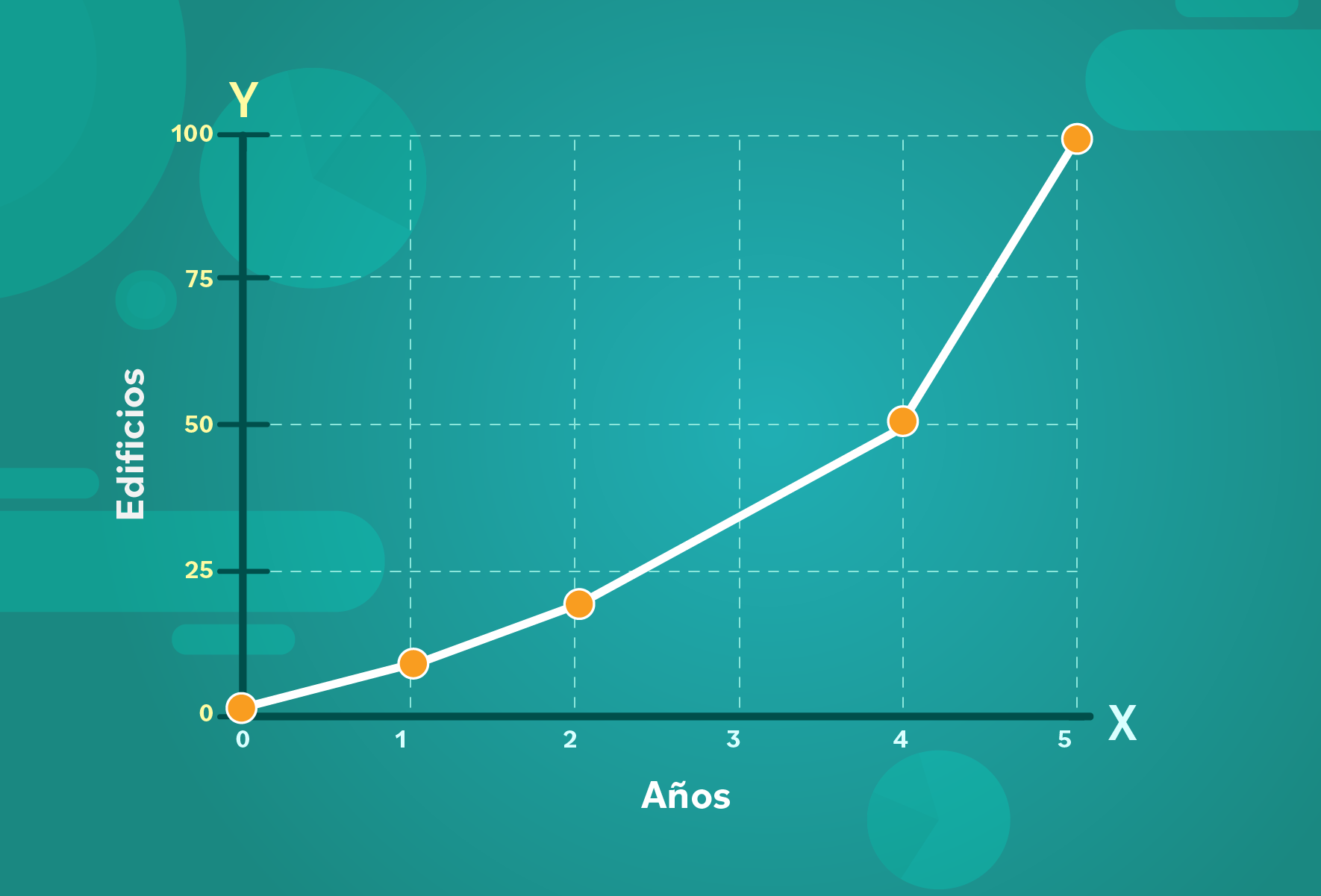
• En el primer año se construyeron 10 edificios.
• A los dos años ya contaban con una ciudadela de 20 edificios.
• En cuatro años, el número de edificios familiares era 50.
• A los 5 años, que era la fecha límite para entregar el proyecto, se habían construido los 100 edificios.

Paso 1: 

Organiza los datos en una tabla, crea una columna para los años y otra para el número de edificios.

Paso 2:

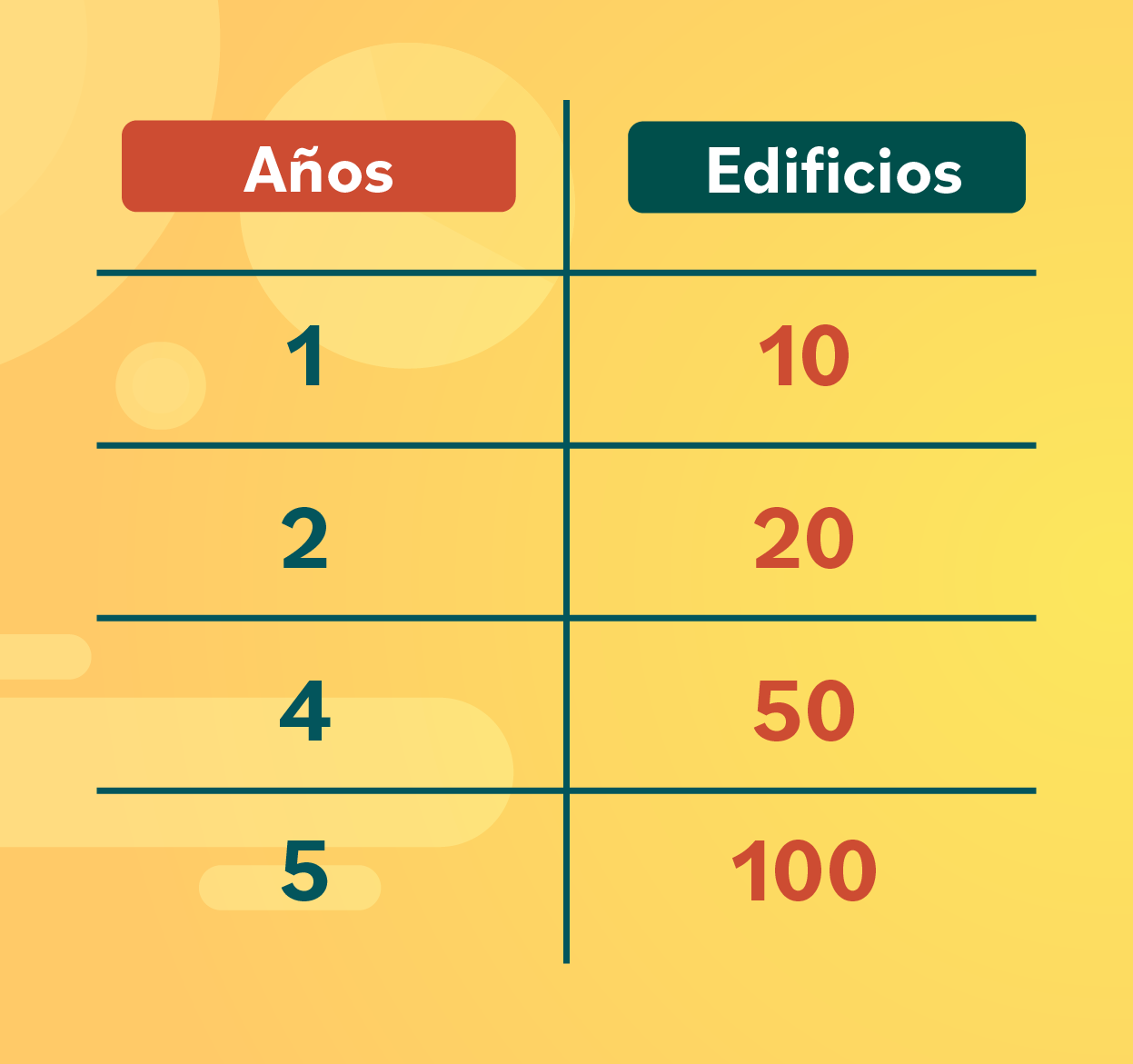
Dibuja el diagrama. En el eje x, ubica la cantidad de años.

Paso 3:

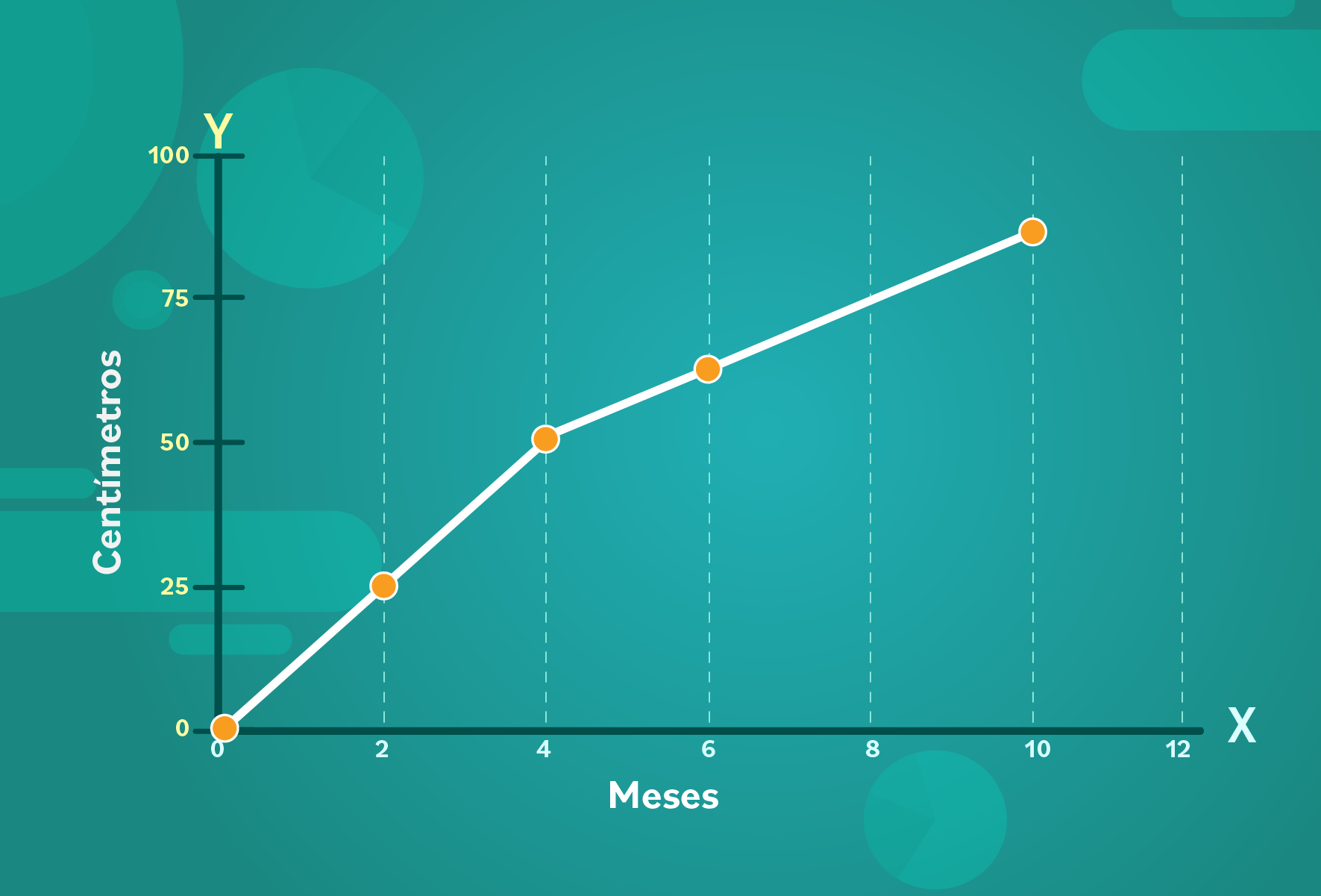
En el eje y, coloca la cantidad de edificios. Puedes usar intervalos de 25, 50, 75 y 100, que es el número más grande.

Paso 4:

Ubica los puntos, según los datos que se cruzan.

Paso 5:

 Y aquí tienes tu gráfico lineal. 

Paso 6: 

Ahora puedes ver cómo creció la construcción de edificios en 5 años. 

– Tendencia central

La tendencia central es otro de los tipos de estadística descriptiva, y se refiere al resumen descriptivo de un conjunto de datos utilizando un único valor que refleja el centro de la distribución de los datos. 

Las medidas de tendencia central también se conocen como medidas de localización central. La media, la mediana y la moda son consideradas las medidas de tendencia central.

La media, que se considera la medida de tendencia central más popular, es el valor medio o más común en un conjunto de datos. La mediana se refiere a la puntuación media de un conjunto de datos en orden ascendente. La moda se refiere a la puntuación o valor más frecuente en un conjunto de datos.

Media, mediana y moda

La media, mediana y moda hacen parte  de las Medidas de Tendencia Central (MTC), usadas en estadística para identificar cuáles son las tendencias en un conjunto de datos  o hacia dónde se inclina o agrupa más la información. Las MTC también son utilizadas para presentar resultados de datos muy extensos, como los estudios que incluyen grandes poblaciones, por ejemplo. 

Gracias a estas medidas, también se pueden proyectar límites o valores hacia los que tiende a inclinarse la variable que estás analizando. ¡Mira cómo funcionan!

Ejemplo: el salón de clases

Aquí tienes una lista con las edades de quince niños que hacen parte de un coro. Como ves, los números son muy variados y están un poco desordenados.

Lo mejor es organizarlos, ya sea de forma vertical u horizontal, así será más fácil calcular las tendencias.

La media

Es el valor promedio del grupo datos, es decir, la cifra que se obtiene al sumar todos los datos y dividir el resultado entre la cantidad de los mismos. 

Paso 1:

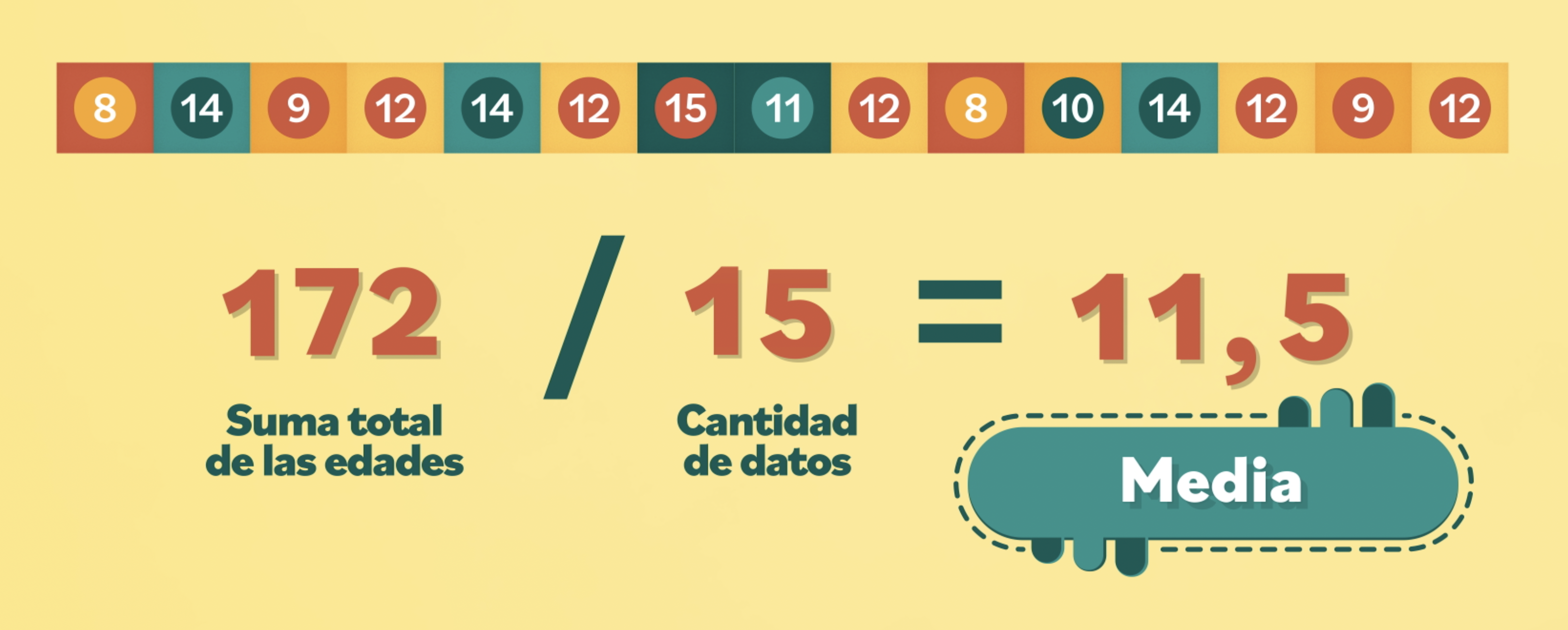
La suma de 8 + 14 + 9 + 12 + 14 y los demás números, es igual a 172.

Paso 2:

Ahora, este resultado hay que dividirlo por la cantidad de datos. Sabemos que tenemos las edades de 15 niños, entonces 172 dividido en 15 es igual a 14, 466666...

Para obtener un número más corto lo que puedes hacer es aproximar. Como el seis es un número mayor a 5, automáticamente el cuatro se aproxima a 5 y así obtienes la media, que es 11,5.

La mediana 

Calcular la mediana es mucho más fácil porque es justo el valor central, es decir, el que se encuentra en la mitad de la lista. 

Paso 1:

Lo único que debes hacer es organizar los datos de menor a mayor o de mayor a menor.

Paso 2: 

Identifica cuál número ocupa el puesto del centro. En este caso la mediana es 12.

Si la cantidad de datos que tienes es impar, como en este ejemplo que son 15 edades, es más fácil identificar el puesto de la mitad. Pero, si llegas a tener un conjunto de datos par, haz lo siguiente:

Paso 3:

Imagina que en la lista no hay 15 edades, si no 16. Ubica los valores de la mitad y súmalos: 

11 + 12 = 23

Paso 4: 

Divide el resultado en dos. 

23 ÷ 2 = 11,5

La mediana es de 11,5.

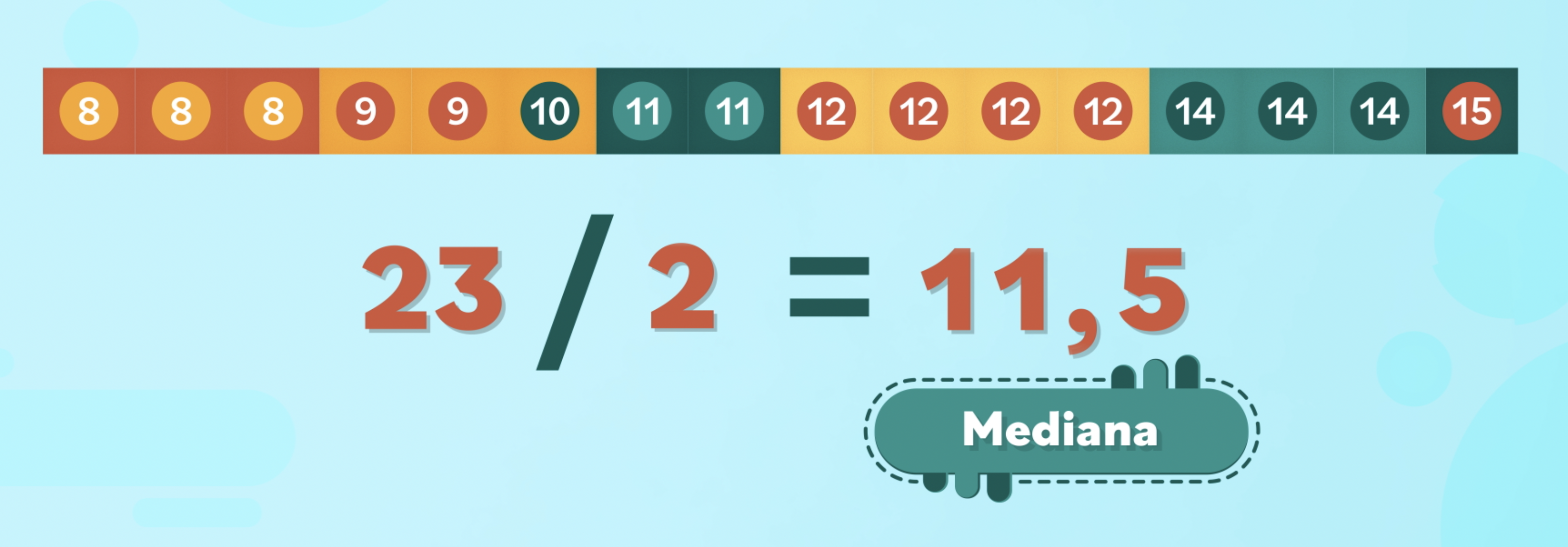
La moda

Es el número que más se repite. Observar esta lista de datos e identifica la cifra que más aparece. 

Si elegiste el 12 es correcto. La moda es 12, porque se repite 5 veces, mientras que el catorce, que es otra cifra que aparece mucho, solo está tres veces. Si tuvieras dos datos que se repiten la misma cantidad de veces, se denomina bimodal.

La próxima vez que necesites calcular la media, la mediana y la moda recuerda lo siguiente:

• Organiza tu conjuntos de datos.
• Para calcular la media solo tienes que sumar todos los datos y dividirlos por la cantidad de datos que tengas.
• Para la mediana, ordena los datos de menor a mayor o viceversa y elige justo el número que se encuentre en la mitad de todos.
• Para la moda, descubre el dato que más se repite.

– Variabilidad

Una medida de variabilidad es una estadística de resumen que refleja el grado de dispersión de una muestra. Las medidas de variabilidad determinan la distancia que los puntos de datos parecen tener con respecto al centro.

La dispersión y la variabilidad se refieren y denotan el rango y la amplitud de la distribución de los valores en un conjunto de datos. El rango, la desviación estándar y la varianza se utilizan, respectivamente, para representar diferentes componentes y aspectos de la dispersión.

El rango representa el grado de dispersión o un ideal de la distancia entre los valores más altos y más bajos dentro de un conjunto de datos. La desviación estándar se utiliza para determinar la varianza media de un conjunto de datos y proporciona una idea de la distancia o la diferencia entre un valor de un conjunto de datos y el valor medio del mismo conjunto de datos. 

La varianza refleja el grado de dispersión y es esencialmente una media de las desviaciones al cuadrado.